
Tessellations are a good topic for an investigation, because as well as the maths involved they also give opportunity for some hands-on design and artistic creativity.
This site has two tools for creating tessellations:
Videos demonstrating how to use these tools are available:
Tessellate! demo
Tessmaker demo
To investigate these, we need to find the interior angles of various regular polygons, and then look for combinations of these angles which add up to 360°.
Here is a worksheet about semi-regular tessellations which I have used with students aged 12-14: Tessellations of Regular Polygons
After completing the worksheet, students can use Tessellate! to create these tessellations. The way in which we choose to colour the tessellation can also have a big impact on how we see it - here is the same tessellation coloured in two different ways:


Tessellate! can also be used for designing patterns which do not strictly follow the rule for semi-regular tessellations. In the example on the left below, the tiles overlap, while on the right the star shapes are not tiles at all, but "holes" in the tessellation:
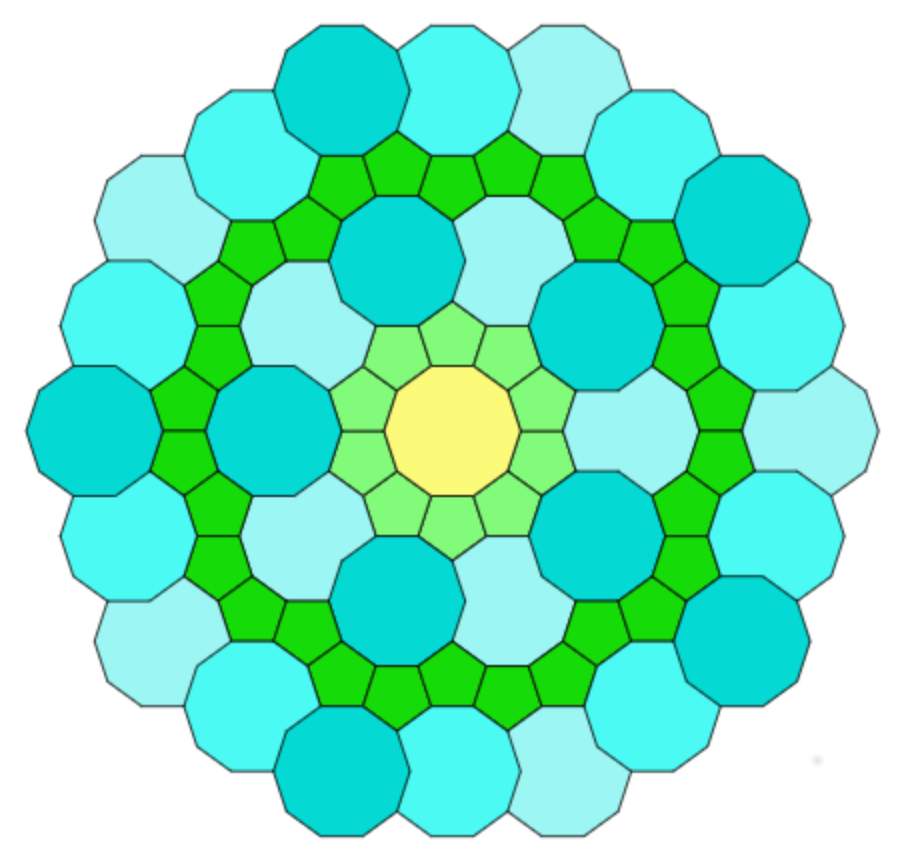

If we use irregular polygons (or shapes with curved sides), there are many possible types of tessellation, which can be classified by their symmetries. Various systems of classification have been used.
TessMaker makes it easy to create 13 different types of tessellation, classified by their "Heesch type". For example we can make designs in the style of Maurits Escher.
Here are some brief instructions:
Here are some examples. The first is an irregular octagon which tessellates by rotation through 60° at some vertices and 120° at others. The second is a re-creation of Escher's "Lizard, 1937".


And here are two created by students, entitled "Ducks" and "Monkey":

